Why the proof of closure under addition in Linear Map is $(T+S)(u+

By A Mystery Man Writer
I am reading Linear Algebra Done Right and want to prove that $L(V, W)$ is a vector space. I have read the solution here: Why the proof of closure under addition in Linear Map is $(T+S)(u+v)$ inst
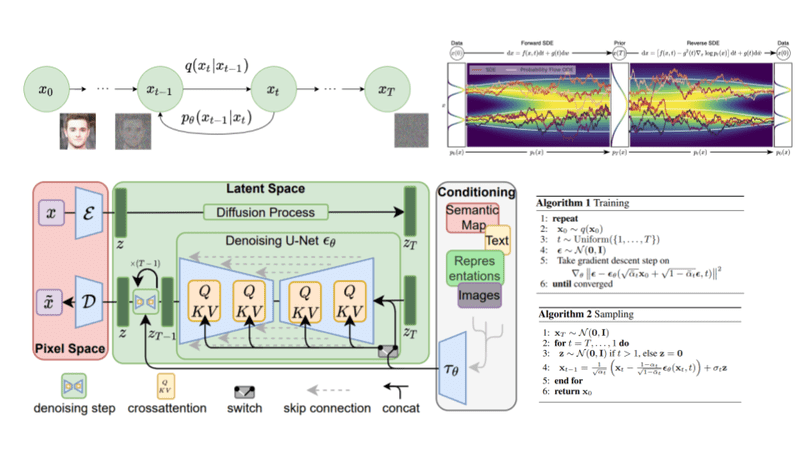
How diffusion models work: the math from scratch
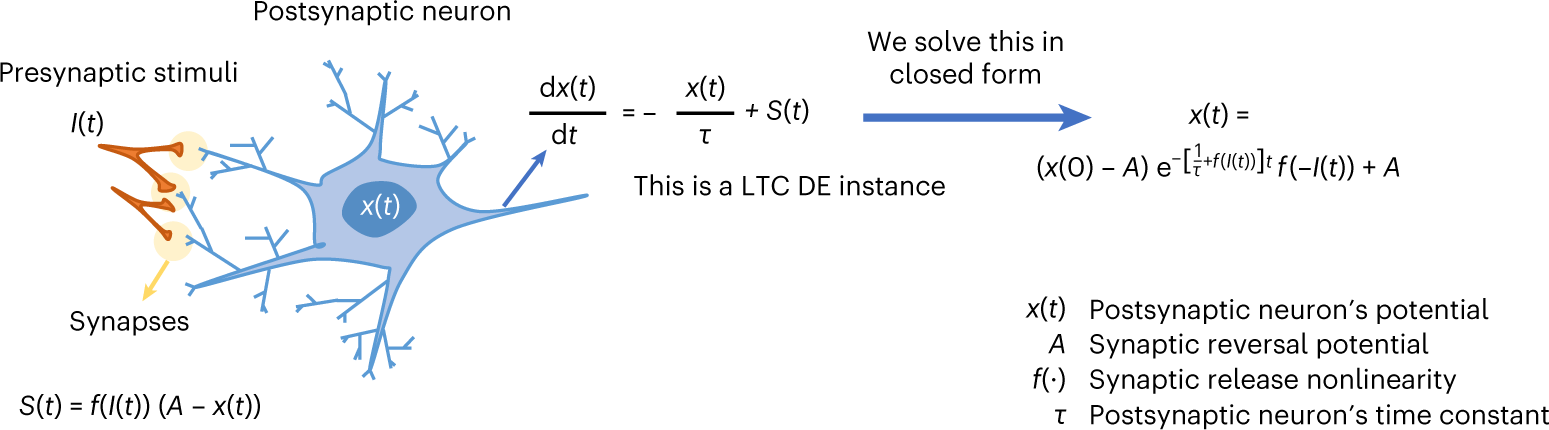
Closed-form continuous-time neural networks
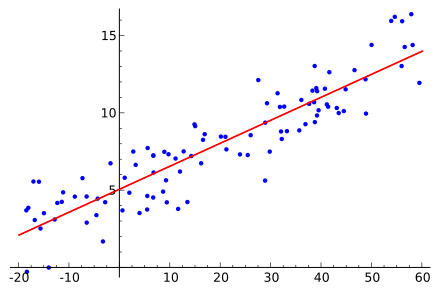
Closed-Form Solution to Linear Regression, by Margo Hatcher

Null Geodesic Congruences, Asymptotically-Flat Spacetimes and Their Physical Interpretation

Linear mapping approximation of gene regulatory networks with stochastic dynamics
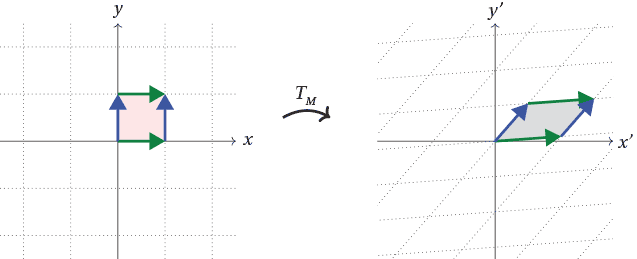
Content - Linear transformations and matrices

Solved Al. Closure under addition: If u, v E V then u +ve V

Proving that a Linear Transformation of a Subspace is a Subspace - Mathematics Stack Exchange
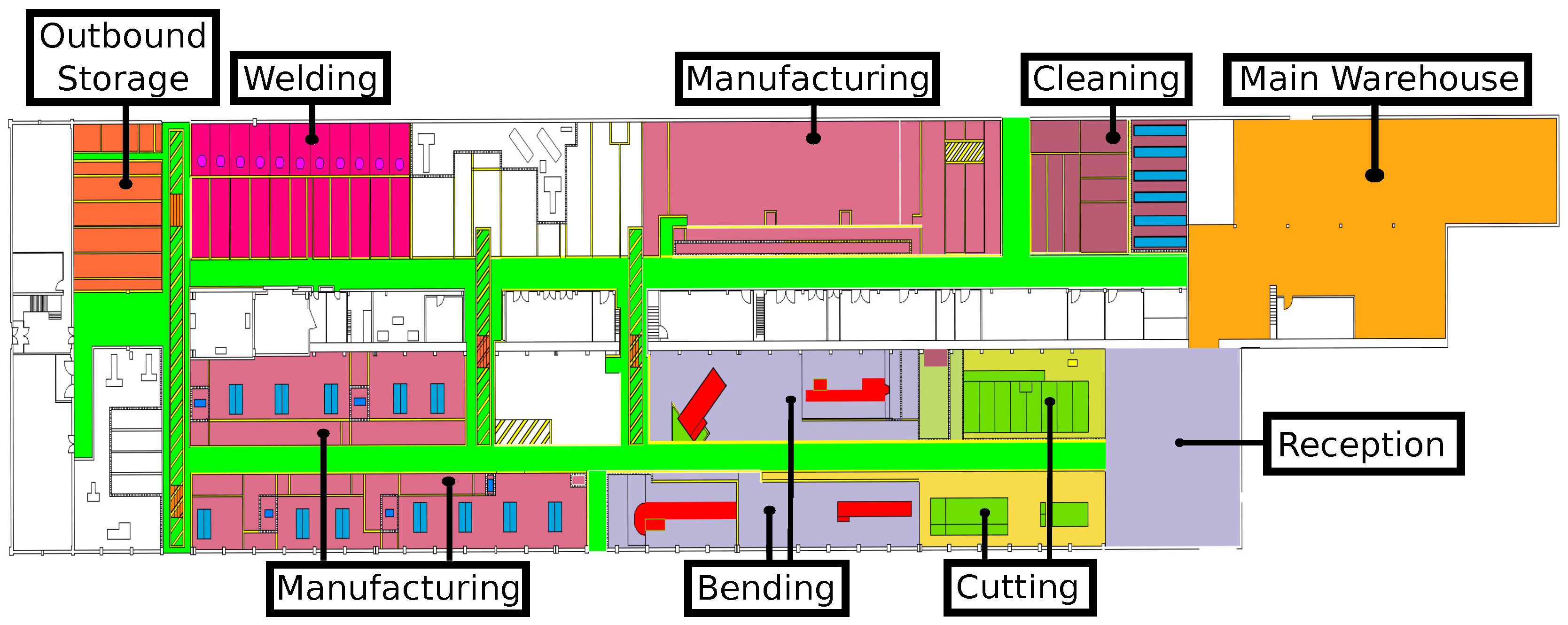
Sensors, Free Full-Text
VSP-0020: ℝn and Subspaces of ℝn - Ximera

Math Properties, Commutative, Associative & Distributive - Lesson

Determine if a set is closed under scalar multiplication

Closure Property, Overview & Examples - Lesson

Set closed under addition, Basic Linear Algebra
- Proof. Unders Period Underwear Brief, Regular Absorbency, Leakproof

- Unders By Proof Period Underwear Briefs - Regular Absorbency - Black - M/l : Target
- Proof Women's Brief Super Heavy Absorbency Period Underwear - Black : Target
- Unders by Proof Incontinence Underwear High Waisted Brief, Heavy Absorbency, Leakproof

- Dramatic Changes to EU Product Liability Rules?

- Lululemon Yoga Leggings Womens 6 Black Ankle Crop Scrunch Up

- Brooks Dare Zip Women's Run Bra for High Impact Running, Workouts and Sports with Maximum Support - Navy - 30A/B : : Clothing, Shoes & Accessories

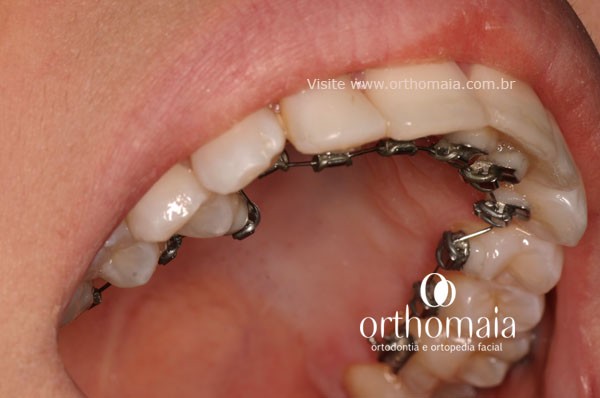
- Aparelho invisível. Tratamento ortodôntico sem sorriso metálico. - Orthomaia.
- Women told to love their saggy boobs and the silicone industry
- Legging Adidas Cintura Alta Essentials Logo



